A trading firm asked me some interesting questions during rounds of phone interview. The rule was to think out loud, and no calculators and paper allowed! Yep, a lot of pressure in the interview. No background questions, just probability and brain teaser questions.
Suppose you were in a betting game. It is given that a treasure chest costs from $0 to $1000. You get the treasure chest if you bet an amount that is equal or higher than its actual value. You could sell the treasure chest to your friend for 50% more its actual value should you get it. How much would you bet?
Solution
The idea here is to maximize the profit. I think most people would think that betting $1000 is good since for sure the treasure chest would be gotten. However, suppose the actual value of the treasure chest is way smaller, then you would lose a lot of money even if you sell it to your friend!
So let’s use the concept of expectation value and probability to decide logically the amount that would optimize the profit.
Suppose I bet $p such that  . Then the probability that I’ll get the treasure chest is
. Then the probability that I’ll get the treasure chest is  .
.
Case 1: Actual value is less than p
Then the expectation value of the actual value is then the half of p, and the expected resell price for my friend is  . The expectation value of the profit is then
. The expectation value of the profit is then  , which occurs
, which occurs  of the time.
of the time.
Case 2: Actual value is more than p
Obviously, there would be no profit in this case and this happens  of the time.
of the time.
Hence the overall expectation value of this game is
 of the time , which is a negative value.
of the time , which is a negative value.
Therefore, this game would likely make someone lose money! So the best way to avoid losing money or maximize the gain is to not bet in this game. So my answer is $0 🙂
Next question is quite a classic brain teaser in probability. I think I’ve seen it when I was a teenager.
Roll a 12-sided die. You and your friend pick a unique whole number from 1 to 12. The player who picked a number closest to the number shown on the die will win. Suppose getting a 12 is 40% and the rest is a uniform distribution of 60%. What number would you pick? Would you choose to be the 1st or 2nd player? Why?
Solution
One of the misleading ways to solve this problem is to choose the whole number closest to the expectation value (8.4). The thing is, if you choose 8 and your friend choose 9, then the your chance of winning is  and your friend’s chance of winning is
and your friend’s chance of winning is  (higher than yours!). This is because 12 is more likely to be shown on the biased die. Thus choosing a number close to 12 is reasonable (i.e. choosing 9, 10 and 11 are worth to consider).
(higher than yours!). This is because 12 is more likely to be shown on the biased die. Thus choosing a number close to 12 is reasonable (i.e. choosing 9, 10 and 11 are worth to consider).
Another catch is to assume that the second player is also smart. If you choose to be the 1st player, your friend (2nd player) would also think of a way to maximize his chance of winning.
So the smart way is to choose to be the 1st player and then pick a right number such that your probability of winning is higher no matter what number the 2nd player choose (if possible).
Fortunately this is possible! By case-by-case trial, this number is 10.
It’s because of the following:
Case 1: 2nd player chose 11
1st player’s chance: 
2nd player’s chance: 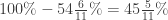
Case 2: 2nd player chose 9
1st player’s chance: 
2nd player’s chance = 
In either case, 1st player’s chance of winning is higher than the 2nd player.
So the being the 1st player and choosing 10 will maximize the chance of winning.

, then the last 2 digits of the product is 75.













